1. 模型变形的方法

在游戏开发中有多种常用技术可以使得一个模型（mesh）变形。比如Blendshape/Morphtarget，可以运行时对顶点插值得到中间状态的模型。比如Linear Blend Skinning，也就是最常见的骨骼蒙皮方法，可以让角色模型变形显示动画。这些技术的目的大多是为了“表现”，将预计算的结果显示出来。而本文涉及的技术，更偏向于“编辑”，也就是预计算的部分。

我们常常会用到“雕刻”的功能，比如在ZBrush中，用笔刷移动模型的局部。不过这种方法相当依赖于用户主观输入，对于程序性的输入支持并不好。而本文中讲到的技术，更加数学严谨。对程序化的建模非常友好。

本文涉及的算法基本都来自于Polygon Mesh Processing一书9.5，9.6节。读者如果想扩展阅读，直接去看这本书就好了。这本书可以说是几何处理的圣经了，作者都是该领域顶级学者。虽然是十年前出版的，但内容一点都不过时。

2.1. 算法回顾-Lattice FFD到Cage FFD

Lattice FFD[Sederberg and Parry 86] 是最经典也是应用最广泛的FFD了，3dsmax和maya都内置了这个功能。它的数学表述为

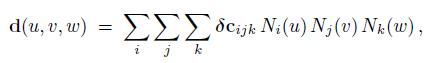
09874f19ca6adb84f9552fdf3c1ec90e.png

其中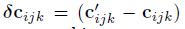，1880c40096a8c2a8d16f9072bf5af7b2.png

是其中一个晶格的控制点。而Ni是一个B样条线的基函数。

上面式子中的u,v,w是某个模型顶点在控制晶格中的局部坐标，即原论文中的s,t,u

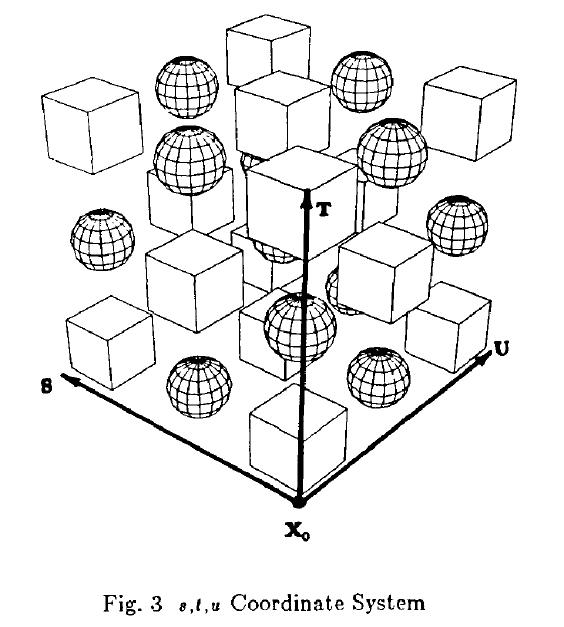
2feb0b8d67dba61bca0db73034fa5758.png

在原始论文中表述为

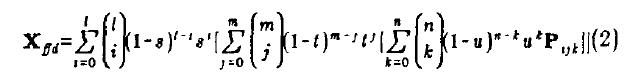
27c7bf846d22e0d97d6ae062c7d83f51.png

直观的可以这样理解：每一个模型顶点都可以通过控制点位置的加权得出。每个控制点对每个顶点的权重，取决于顶点在控制点坐标系下的坐标，在经典FFD中是一个B样条基函数的权重。

因为权重只取决于初始几何位置，可以预先计算，因此变形时计算很快。

经典FFD的问题是控制点是晶格的，对于造型比较复杂，在包围盒中有很多多余空间的模型，会造成很多控制点的浪费。因此有人提出了Cage-Based FFD

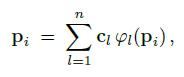
c05d52e069e1a5d9375544dc619acfe7.png

其表述与经典FFD基本一致。权重仍然只与位置相关。只不过，这里控制点的权重不是用B样条基函数计算的，而被称为广义重心坐标(generalized barycentric coordinates).

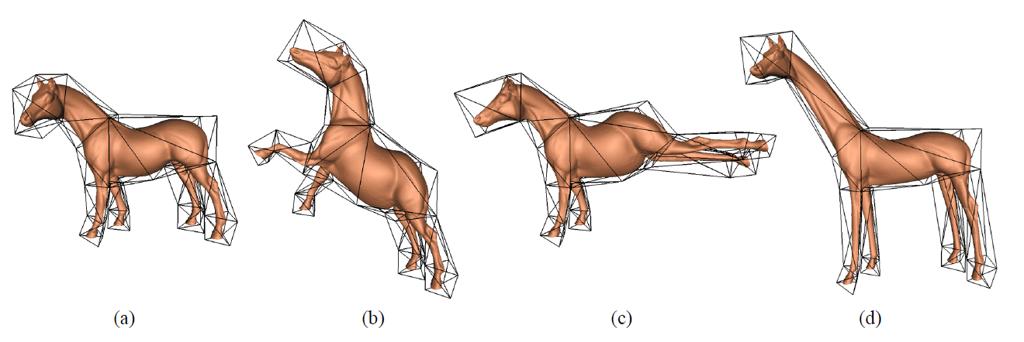
cde8ba37859c6329baae9f290fa7eec4.png

不过其坐标的计算相当复杂，这里不再赘述了

FFD存在的一个问题是如果给定某点位移作为限制条件，其结果会有缺陷。

我们假定有N个控制点，M个约束坐标点。这M个点的位移大小我们给出了限定，但我们不知道控制点如何位移才能得到这M个点

这相当于解一个线性方程

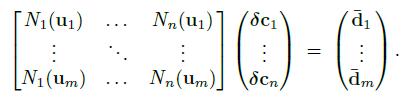
31a7f2be12c5f35674c39526af81cc4e.png

注意Ni权重是确定的，di是M个点的位移是我们限定的，如果想要求每个控制点的位移，由于m和n不一定相等。如果m太多，那么解无法满足只能成为最小二乘解。如果n太多那么它倾向于最小化控制点位移，而不是使得目标模型平滑。

如果我们回忆一下Linear Blend Skinning即骨骼蒙皮的做法，其变形原理也是对控制点（如果认为骨骼是控制点）的加权移动。区别在于骨骼蒙皮的权重是稀疏的，一般只有4-8个权重不为0。而且骨骼蒙皮的权重是可以自由定义的，即用户可以刷权重，而不是被数学公式定义的。

2.2. RBF变形

RBF的表述为下式

Image.png

注意其中phi是基函数，他可以有很多种形式，但不变的是它与控制点到变形点的距离相关。在这个式子中，它相当于一个几何的权重值。

需要注意的是alpha这个值，它不是一个预计算的常量。它是一个需要被求解的向量。最后一项P是一个多项式补偿量。

它有两个边界条件：

第一个，对控制点用RBF变形的结果，与它移动距离相等。

Image-1.png

第二个，对原点变形还是原点（一定需要吗？）

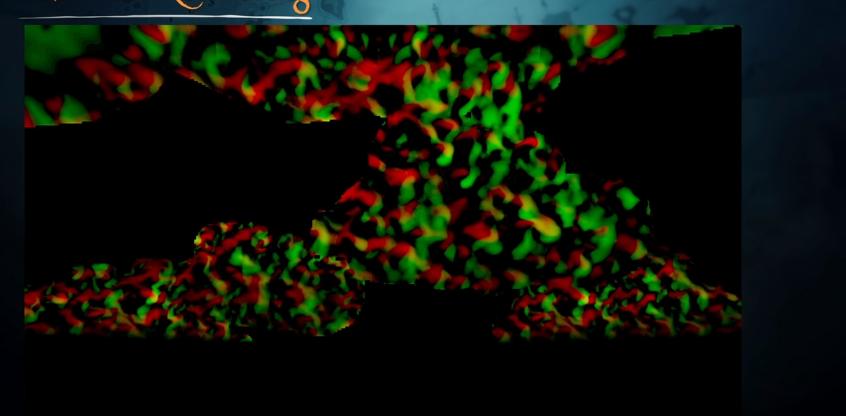
Image-2.png

以上两个条件可以写成矩阵，我们求解它就行了。

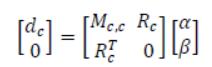
438e6a838bd3480fc62b834ca67aaa7b.png

其中，Mc,c是控制点相互的基函数

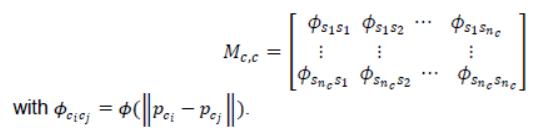
90fe7218fbc07798411c566ce302339f.png

alpha是待求的向量权重，beta是待求的多项式系数，Rc是控制点的坐标，dc是控制点的位移。

需要注意的是，每次控制点变形，都要求解一遍系数的。因此RBF计算速度会相对较慢，但它的好处是

  1. 控制点可以是随意形状
  2. 变形位置与控制点很接近，因为控制点变形满足边界条件

作为对比，可以看3dsmax中的FFD，一是只有lattice和圆柱两种，而是被变形的点甚至不跟着控制点走

相比之下maya的FFD(Lattice)更好一些。

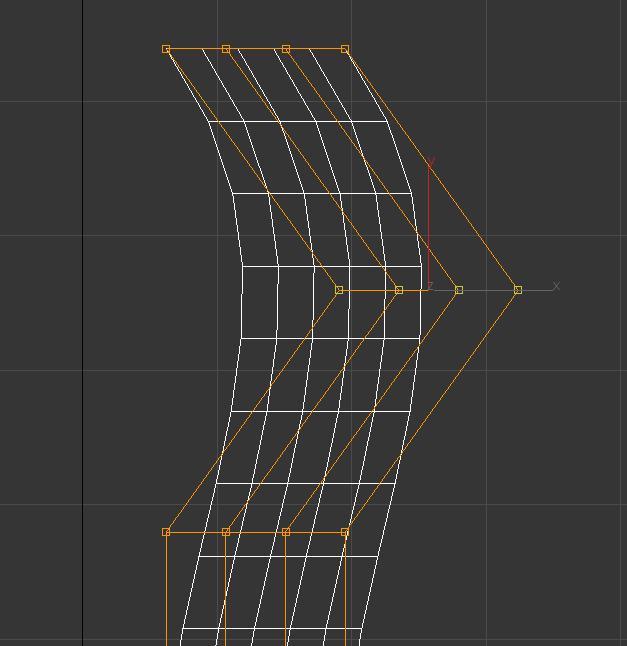
3d5041b9f605dc354f2bb3d7cc8a92e2.png

2. Houdini中的实现

由于需要解一个线性方程，可以用numpy.linalg来做，这里写了一个python节点，其实也只需要一个python节点

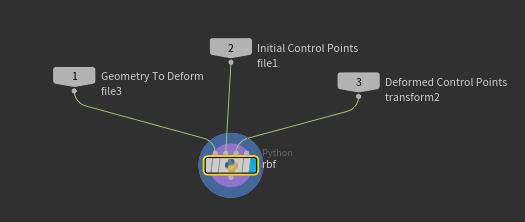
959a6768fd563561a57578834951bb30.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
node = hou.pwd()
geo = node.geometry()

import numpy as np

# Add code to modify contents of geo.
# Use drop down menu to select examples.

# input N*3 float for N pts, M*3 float for M pts
# output N*M*3 float for cross-ref distance    
def cdist(x,y):
    npts1 = x.shape[0]
    npts2 = y.shape[0]
    expander_src = np.ones(shape = (1,npts2,3))
    expander_dst = np.ones(shape = (npts1,1,3))
    src = np.expand_dims(x,1)
    dst = np.expand_dims(y,0)
    diff = -src*expander_src+  dst*expander_dst
    return np.sqrt(np.sum(diff * diff, axis=2))

def rbf(dist, r):
    h = dist/r
    d = np.clip(1-h,0,1)
    return d*d

#reshape inputs
ctrl_source = node.inputGeometry(1)
ctrl_target = node.inputGeometry(2)
npts = len(ctrl_source.points())
assert(len(ctrl_source.points()) == len(ctrl_target.points()))
ctrl_source_pts = np.array(ctrl_source.pointFloatAttribValues("P")).reshape(npts,3)
ctrl_target_pts = np.array(ctrl_target.pointFloatAttribValues("P")).reshape(npts,3)

#placeholder
MR = np.zeros([npts+4, npts+4])
D = np.zeros([npts+4, 3])

dist = cdist(ctrl_source_pts,ctrl_source_pts)
R_c = np.insert(ctrl_source_pts,0,1,axis=1)

#right term
MR[:npts, :npts] = rbf(dist, 1)
MR[:npts, npts:] = R_c
MR[npts:, :npts] = R_c.T

#left term
D[:npts,:] = -ctrl_source_pts + ctrl_target_pts

#solved weights, concatenation of alpha and beta
x = np.linalg.solve(MR,D)

#reshape inputs
deform_mesh = node.inputGeometry(0)
deform_npts = len(deform_mesh.points())
deform_pts = np.array(deform_mesh.pointFloatAttribValues("P")).reshape(deform_npts,3)

dist = cdist(deform_pts,ctrl_source_pts)

#rbf weights
M = np.zeros([deform_npts,npts+4])
M[:,:npts] = rbf(dist, 1)
M[:,npts:] = np.insert(deform_pts,0,1,axis=1)

deform_pts +=  np.matmul(M,x)

geo.setPointFloatAttribValues("P", deform_pts.reshape(3*deform_npts));

3. 应用

第一个例子对一个怪兽头部做了变形

由于控制点可以程序化控制，这里对控制点做了一个噪波，变形出了很多种

monster.jpg

节点：

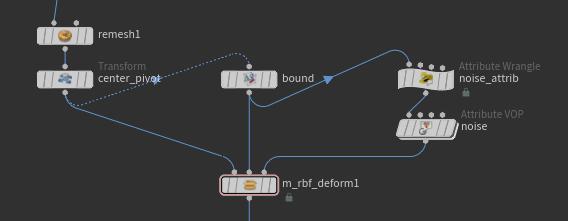
6d6a36f10e72423914d10235c97bc777.png

第二个例子中，由于控制点可以是任何形状，甚至任何blendshape都可以

因此可以对不同体型的衣服做变形

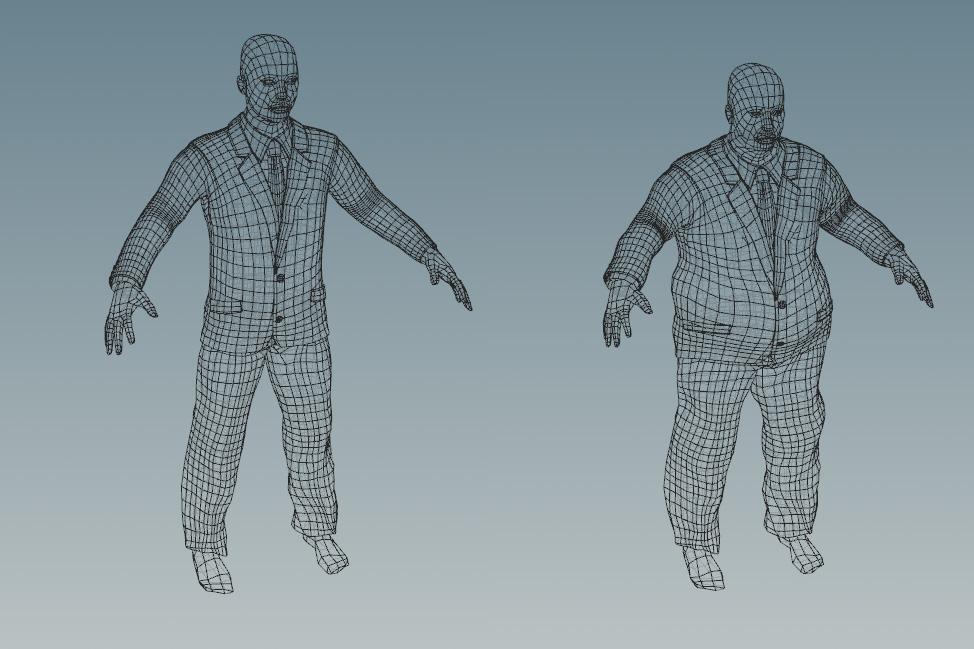
deform_suite.jpg

左为原始身体+原始衣服，右为新的身体+变形后的衣服

节点也很简单

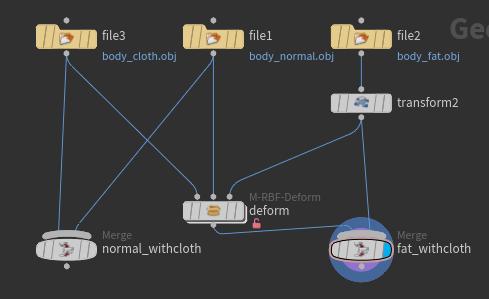
deform_person_node.PNG

Reference

Free-Form Deformation of Solid Geometric Models

Ju T , Schaefer S , Warren J . Mean value coordinates for closed triangular meshes[J]. ACM Transactions on Graphics, 2005, 24(3):561.

Boer A D, Schoot M S V D, Bijl H. Mesh deformation based on radial basis function interpolation[J]. Computers & Structures, 2007, 85(11):784-795.

Bogdan Cosmin Mocanu. 3D mesh morphing. Economies and finances. Institut Nationaldes Télécommunications,2012.English