我们常用法线贴图模拟表面的细节凹凸,不过法线贴图的一个问题是在视角很低(Gazing Angle)时会出现失真
主要原因是法线贴图不会考虑高度的遮挡关系,因此有一些被遮挡的面会被渲染出来。解决这一问题的方法主要有两种,
- Tessellation, 通过细分增加面数,使得面片具有高度。
- POM/Relief,通过在贴图空间中根据视线的方向,通过与高度图求交,获取到真实应该采样的UV坐标。
第一种方式增加了顶点和面数,对vertex/hull tess压力较大,而后一种由于需要多次采样高度图,对pixel shader压力较大。以下主要讨论POM/Relief的原理和一些修正。
最早是2001年Kaneko给出了Parallax的定义,论文提出使用偏移UV的方式采样贴图,UV的偏移值是正比于采样处的高度的。这种方法后来被称为Offset-Limiting。这种偏移UV的方式比较简单,而且开销很低,对于高度图变化比较平缓的情况比较适用。比如在眼球的shader中,用于虹膜的渲染。
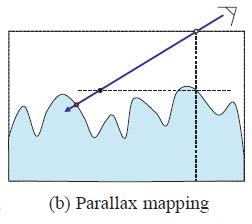
但是Offset-Limiting只是对UV偏移的一个简单拟合,并不是很精确。后来的文章主要在精确求解UV的偏移量。
比如2015年的时候,McGuire提出了的Steep Parallax Mapping。这是一种RayMarching的方式,每步前进查找高度图是否已经低于当前采样处高度。选择最后一步的uv。
不过注意这种算法没有精确找到相交的高度,只是找到了一个小于步长的近似值。
对Steep Parallax Mapping的改进是Tatarchuk提出的Parallax Occulusion Mapping, 同样是raymarching固定步长采样高度图,不过最后一步会进行一个插值,这样结果更精确。注意这个Tatarchuk就是Natalya Tatarchuk,娜姐,目前在Unity做Graphic Director。写POM的时候还是ATI的工程师,后来在Bungie工作过。
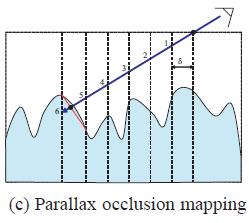
我们都知道,对于求解的问题,二分查找比线性查找时间复杂度是小的。
因此POLICARPO提出了Relief Mapping。开始是线性步长查找,不过步长可以更大。当第一次相交后,再进行二分查找。这样在同样步数的情况下查找更为精确。
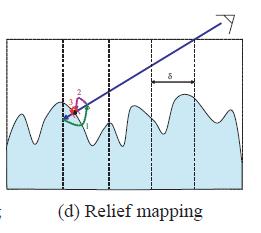
后面还有一些微小的改进,不过已经无关紧要了。POM/Relief对大多数情况已经足够了。
当然还有一些文章为了解决这个高度渲染的问题另辟蹊径。
比如DONNELLYW提出用有符号距离场SDF做Raymarching,更加精确,模型也很简洁,缺点是贴图比较大。
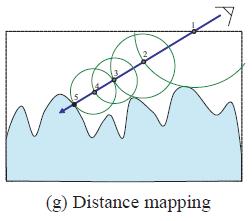
比如WANG提出VDM,从不同视角存了高度图,相当于一个五维的置换贴图。
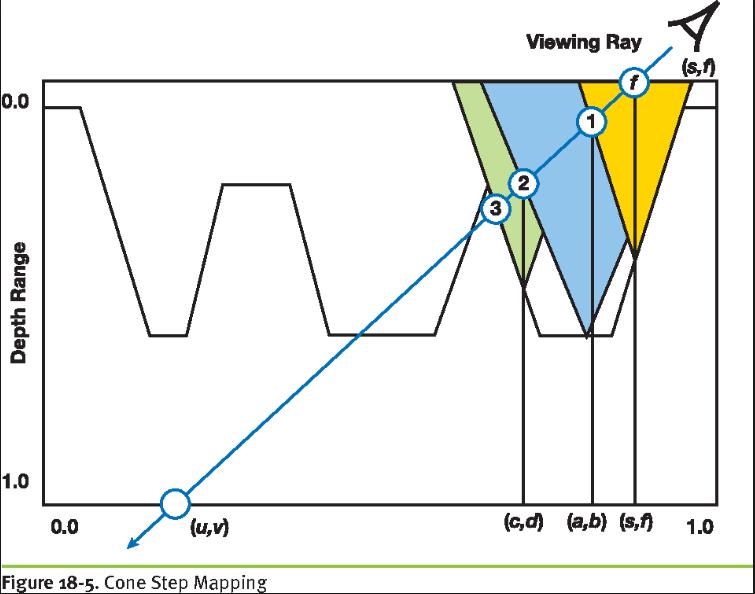
比如Policarpo提出的Cone Step Mapping,预处理生成一张ConeMap就可以减少RayMarching求解的步数。
继续回到话题,POM/Relief遇到的一个问题是轮廓无法正确渲染,因此有人提出了一些优化
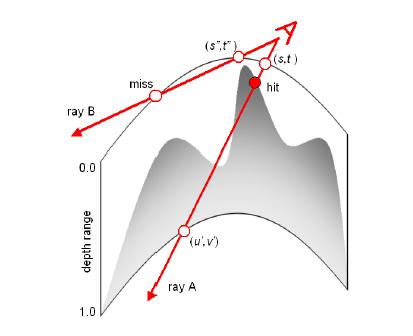
Oliviera提出我们用二次曲面拟合模型的局部,切线空间计算时用采样点处的二次曲面曲率偏移视线。
这对于简单的可以用二次曲面拟合的,并且UV和曲率方向一致的曲面比较容易,比如球面,圆柱面。但是对于一般曲面容易出现问题。
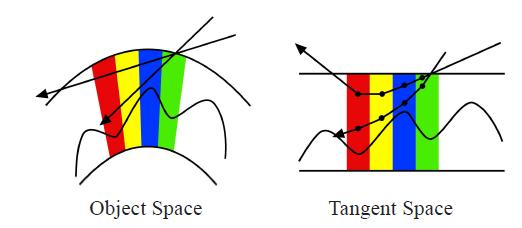
有这种变形高度图的,自然也有变形视线的。但是问题是需要这就需要每一步重新计算切线空间的视线方向,也就必须要把ObjectSpace的法线和切线烘成贴图,每步重新计算TBN。开销就更大了。
以及Hirche提出了后来衍生为被称为Shell Mapping的技术,沿线框方向挤出一个面(Prism),在这个棱锥里面进行raytracing。这种后来又衍生为Prism Parallax Mapping
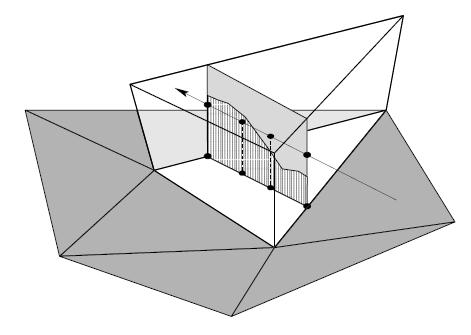
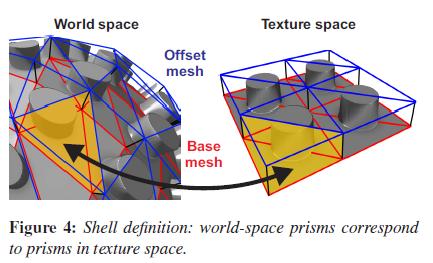
当然这样面数开销比较大,要用上Geometry Shader,但好处是通用性比较强。
至此就没什么新鲜的关于POM技术的研究了,这个时候是2007年。
参考资料:
Real-time Rendering, 4th Edition, Chapter 6-8
最早提出Parallax Mapping
Kaneko, Tomomichi, et al. “Detailed shape representation with parallax mapping.” Proceedings of ICAT. Vol. 2001. 2001.
Steep Parallax Mapping:
McGuire, Morgan, and Max McGuire. “Steep parallax mapping.” I3D 2005 Poster (2005): 23-24.
POM:
Tatarchuk, Natalya. “Dynamic parallax occlusion mapping with approximate soft shadows.” Proceedings of the 2006 symposium on Interactive 3D graphics and games. ACM, 2006.
Relief:
Policarpo, Fábio, Manuel M. Oliveira, and João LD Comba. “Real-time relief mapping on arbitrary polygonal surfaces.” Proceedings of the 2005 symposium on Interactive 3D graphics and games. ACM, 2005.
Distance Function:
Donnelly, William. “Per-pixel displacement mapping with distance functions.” GPU gems 2.22 (2005): 3.
VDM:
Wang, Lifeng, et al. “View-dependent displacement mapping.” ACM Transactions on graphics (TOG). Vol. 22. No. 3. ACM, 2003.
Cone Step Mapping:
Policarpo, Fabio, and Manuel M. Oliveira. “Relaxed cone stepping for relief mapping.” GPU gems 3 (2007): 409-428.
Curved Relief Mapping
Oliveira, Manuel M., and Fabio Policarpo. “An efficient representation for surface details.” Instituto de Informatica UFRGS (2005).
Shell Mapping:
Hirche, Johannes, et al. “Hardware accelerated per-pixel displacement mapping.” Proceedings of Graphics interface 2004. Canadian Human-Computer Communications Society, 2004.
Porumbescu, Serban D., et al. “Shell maps.” ACM Transactions on Graphics (TOG) 24.3 (2005): 626-633.
Catlike Coding教程,Unity中实现POM/Relief
https://catlikecoding.com/unity/tutorials/rendering/part-20/
UE4中的POM:
https://wiki.unrealengine.com/Parallax_Occlusion_Mapping
UE论坛上对POM的讨论
https://forums.unrealengine.com/development-discussion/rendering/19743-pom-material/page18
CryEngine的SPOM,使用了Prism的技术
https://docs.cryengine.com/display/SDKDOC2/Silhouette+POM
Unity论坛中讨论CRM
https://forum.unity.com/threads/fabio-policarpo-relief-mapping-with-correct-silhouettes.32451/
Github上一个对不同POM/Relief原理的文档,有代码