背景是公司内部的一个比赛：Taichi 99 行代码体素挑战。使用代码创建体素艺术。笔者提交的作品获得了头名，比较有意思，因此讲讲这个作品。
代码在此： maajor/maajor-voxel-challenge (github.com)
比赛的限制条件是：128x128x128的体素空间；99行taichi代码；不能用别的库；不能导入文件。但是笔者想搞一个具象的，复杂的东西，容易引起人共鸣的作品，而笔者只有一天时间。
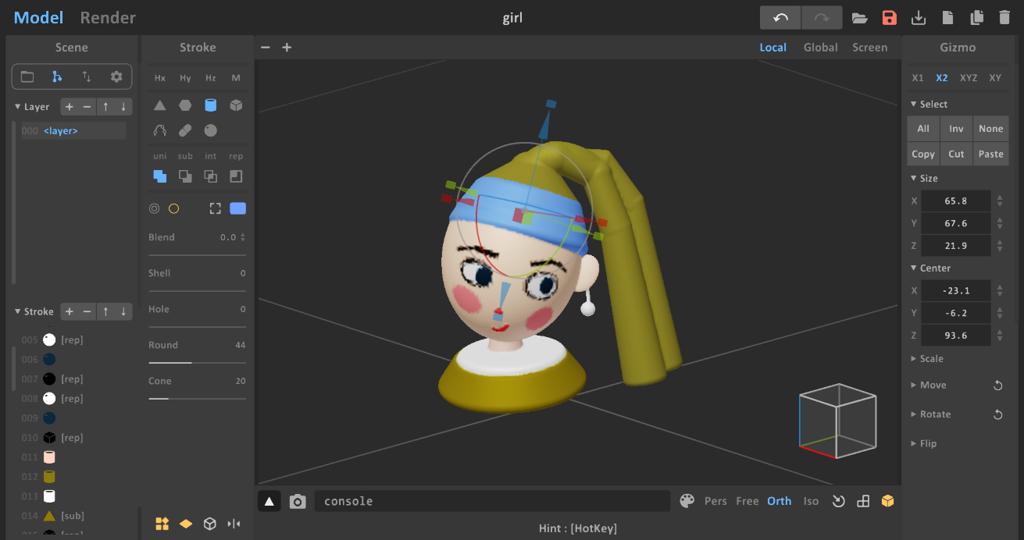
想了想就是珍珠耳环的少女了，这幅画相对简单又比较有名，而且恶搞很多。
1. How
所以具体怎么做的？具体如下
1.1 使用MagicaCSG创建
如果你不知道MagicaCSG是啥，戳这里：MagicaVoxel (ephtracy.github.io) 一个轻量级CSG编辑器。
它的原理就是用基本型（球、圆柱、方块和棱锥）拼装成目标形状。
不过笔者目前的实现里只支持球、圆柱、方块和棱锥。暂时不支持SDF Blend和其他基本形。混合方式支持Uni, Sub, Rep三种
因此笔者先在编辑器里做出一个目标效果
然后将它导出mcsg一个文件。文件的定义只是Primitive的定义，类似如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
"csg" : [ [ { "type" : "sphere" "rgb" : "255 217 187" "round%": "0.1" "line_w": "1" "r" : "0.728571 0.670834 -0.13844 -0.679403 0.682019 -0.27067 -0.0871557 0.291259 0.952666" "t" : "-21.6247 -16.4945 71.7355" "s" : "34.4496 35.9258 41.8245" "tube" : "1" } ... |
1.2 在Taichi中实现基本型
这里极大收到了IQ的文章启发：Inigo Quilez :: computer graphics, mathematics, shaders, fractals, demoscene and more，
使用SDF表示几何体。不过IQ文章里的公式缺一些参数，比如cone，top_v等等，笔者尝试自己实现。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
@ti.func def elli(rx,ry,rz,p1_unused,p2_unused,p3_unused,p): r = p/vec3(rx,ry,rz); return ti.sqrt(dot(r,r))<1 @ti.func def cyli(r1,h,r2,round, cone, hole_unused, p): ms=min(r1,min(h,r2));rr=ms*round;rt=mix(cone*(max(ms-rr,0)),0,float(h-p.y)*0.5/h);r=vec2(p.x/r1,p.z/r2) d=vec2((r.norm()-1.0)*ms+rt,ti.abs(p.y)-h)+rr; return min(max(d.x,d.y),0.0)+max(d,0.0).norm()-rr<0 @ti.func def box(x, y, z, round, cone, unused, p): ms=min(x,min(y,z));rr=ms*round;rt=mix(cone*(max(ms-rr,0)),0,float(y-p.y)*0.5/y);q=ti.abs(p)-vec3(x-rt,y,z-rt)+rr return ti.max(q, 0.0).norm() + ti.min(ti.max(q.x, ti.max(q.y, q.z)), 0.0) - rr< 0 @ti.func def tri(r1, h, r2, round_unused, cone, vertex, p): r = vec3(p.x/r1, p.y, p.z/r2);rt=mix(1.0-cone,1.0,float(h-p.y)*0.5/h);r.z+=(r.x+1)*mix(-0.577, 0.577, vertex) q = ti.abs(r); return max(q.y-h,max(q.z*0.866025+r.x*0.5,-r.x)-0.5*rt)< 0 |
我们只要保证在MagicaCSG中参数对应的效果和我们自己构造的基本型效果一致就可以了
1.3 生成Taichi代码
所以其实mscg文件中每一个primitive应该对应taichi代码的一行。
see: maajor-voxel-challenge/mcsg_to_py.py
这一步只要将坐标变换调对即可，也不复杂。基本原理就是
|
1 2 3 4 5 |
foreach primitive in mscg_file: line_of_code = makecode(primitive.parameters) code.append(line_of_code) file.write_all_lines(code, "out.py") |
然后命令行调用，将刚才导出的mcsg文件变成python代码。
|
1 |
python3 mcsg_to_py.py -i somefile.mcsg -o main.py |
最后生成的代码大概长成
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
@ti.func def elli(rx,ry,rz,p1_unused,p2_unused,p3_unused,p): blablabla... @ti.func def make(func: ti.template(), p1, p2, p3, p4, p5, p6, pos, dir, up, color, mat, mode): blablabla... @ti.kernel def initialize_voxels(): make(elli,35.9,41.8,34.4,0.0,0.0,0.0,vec3(-16,8,-22),vec3(0.3,1.0,-0.1),vec3(0.7,-0.3,-0.7),rgb(255,217,187),1,0) make(cyli,33.8,10.9,32.9,0.4,0.2,0.0,vec3(-6,30,-23),vec3(0.4,0.9,-0.1),vec3(0.9,-0.4,0.0),rgb(114,161,255),1,0) make(elli,11.1,10.6,2.9,0.0,0.0,0.0,vec3(-23,-17,8),vec3(0.4,0.8,0.6),vec3(0.9,-0.4,-0.1),rgb(255,141,143),1,2) make(elli,10.2,7.7,15.3,0.0,0.0,0.0,vec3(-45,-4,-18),vec3(-0.4,0.9,0.2),vec3(0.1,-0.2,1.0),rgb(255,141,143),1,2) ....... |
2. Why
体素挑战有很多种参加方式：写代码，程序化艺术，分型，etc。为什么要用这种方法，借助数字内容创作工具（DCC），而不纯写代码？
有三点很重要：好理解，快速反馈和重用。
- 好理解：不需要掌握复杂的procedural/分型算法，点几下鼠标就能做出一个东西。使用MagicaCSG就有这个好处。
- 快速反馈：调整基本型的位置如果能实时预览到效果，不需要改参数再编译。这里使用MagicaCSG，节约了很多基本型的参数调整时间，笔者只花了一天就做出来了。
- 重用：重用原型减少工作量。这里使用CSG的建模方式，用基本型就能拼装出结果。
这样任何一个人不用写代码，只需要操作DCC工具就能快速产出结果参加体素挑战。因此笔者作品相比于其他作品，算法的复杂度比较低，上手门槛比较低，而且能制作的自由度较高，比较容易引起观者的共鸣。
笔者认为，让图形计算惠及每一人的方法不只是写代码，更重要的是可交互创作工具。这样才能让任何人，快速产出复杂的效果。
3. 结论
笔者确实很快完成了这个项目，大概只花了一天。虽然功能不是很全，没有SDF融合，并且一些效果无法实现，比如变形，噪声等。在MagicaCSG中无法预览。
但是基本完成了Proof of Concept： 使用数字内容创作工具可以快速高质量完成体素挑战。
降低创作门槛，解放创造力。这是笔者所在公司太极图形的使命，太极开物云平台努力践行这一梦想。
最后是招人广告，寻
- 软件开发工程师，对DCC工具开发感兴趣，熟悉Unity或者UE即可。
- 技术美术，对DCC工具开发感兴趣，熟悉程序化即可，请附作品集。
公司地点在北京中关村或者上海张江科技园，深圳办公室在筹备中也会考虑。
